Dua konsep penting dalam matematika yang berkaitan dengan kemungkinan terjadinya suatu peristiwa, contoh kasus peluang dalam membeli telur. Peluang adalah ukuran yang menunjukkan seberapa besar kemungkinan terjadinya suatu peristiwa, seringkali diungkapkan sebagai persentase atau fraksi. Di sisi lain, kombinatori adalah cabang matematika yang mempelajari pengaturan, permutasi, dan kombinasi objek. Dalam konteks soal ini, kita menggunakan prinsip-prinsip kombinatori untuk menghitung peluang memilih telur yang tidak busuk dari sebuah keranjang yang mengandung campuran telur busuk dan tidak busuk. Ini adalah contoh praktis bagaimana teori peluang dan kombinatori dapat diterapkan dalam kehidupan sehari-hari, memberikan wawasan tentang bagaimana keputusan dapat dibuat berdasarkan kemungkinan hasil yang berbeda.
Table of Contents
Contoh Soal Membeli Telur
andi diminta ibunya untuk membeli telur, saat memilih sebuah keranjang ternyata yang dipilih di dalamnya terdapat 2 telor busuk dari 25 telor yang ada di dalam keranjang tersebut. andi ingin membeli 3 telor dengan cara mengambil 3 sekaligus secara sembarang dari dalam keranjang tersebut. peluang terambil semua telor tidak ada yang busuk adalah?
Jawaban Soal Membeli Telur
Peluang bahwa ketiga telur yang diambil Andi tidak busuk adalah 0.77 atau 77%. Ini berarti Andi memiliki kesempatan 77% untuk memilih 3 telur yang semuanya tidak busuk dari keranjang tersebut.
Pembahasan
Soal andi membeli telur tersebut berkaitan dengan peluang dan kombinatori. Untuk menemukan peluang bahwa ke 3 telur yang diambil oleh Andi tidak busuk, kita dapat menggunakan prinsip kombinatori dasar.
Ada 25 telur di keranjang, dengan 2 di antaranya busuk dan 23 yang tidak busuk. Andi ingin mengambil 3 telur secara acak. Peluang untuk tidak mendapatkan telur busuk sama dengan jumlah kombinasi mengambil 3 telur yang tidak busuk dibagi dengan jumlah kombinasi mengambil 3 telur secara acak dari keseluruhan 25 telur.
Menghitung Kombinasi Telur Tidak Busuk
Kita ingin tahu berapa banyak cara kita bisa memilih 3 telur dari 23 telur yang tidak busuk. Ini adalah kombinasi, karena urutan pengambilan tidak penting.
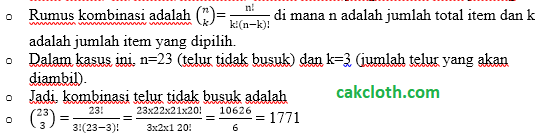
Menghitung Total Kombinasi
Sekarang, kita ingin tahu berapa banyak cara kita bisa memilih 3 telur dari semua 25 telur (termasuk yang busuk).

Menghitung Peluang
Peluang mendapatkan 3 telur yang tidak busuk adalah rasio dari “jumlah kombinasi memilih 3 telur tidak busuk” terhadap “total kombinasi memilih 3 telur dari semua 25 telur”.
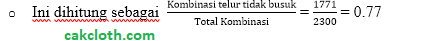
Dalam bahasa pemrograman yang digunakan saat menghitung nilai-nilai ini, didapatkan hasil bahwa peluang Andi mendapatkan 3 telur yang tidak busuk adalah 0.77 atau 77%. Ini berarti, jika Andi memilih 3 telur secara acak dari keranjang, ada kemungkinan 77% bahwa ke 3 telur tersebut akan tidak busuk.
Tambahan
Dari contoh soal andi membeli telur diatas, Kita perlu memahami apa itu “faktorial”, dibawah ini adalah penjelasanya.
Faktorial Adalah
Faktorial dari sebuah bilangan, yang ditulis sebagai n! (dibaca “n faktorial”), adalah hasil kali semua bilangan bulat positif dari 1 sampai n. Jadi, 23! (23 faktorial) adalah hasil kali semua bilangan bulat dari 1 hingga 23.
Perhitungannya adalah: 23! = 23 × 22 × 21 × 20 × 19 × … × 3 × 2 × 1
Ini adalah perhitungan yang sangat besar dan hasilnya adalah angka yang sangat besar. Mari kita hitung nilai tepatnya.
Hasil dari perhitungan 23! (23 faktorial) kurang lebihnya di angka 25852016738884976640000. Ini adalah jumlah angka yang sangat besar yang dihasilkan dari perkalian semua bilangan bulat dari 1 hingga 23. Faktorial sering digunakan dalam perhitungan kombinasi dan probabilitas karena menyatakan berapa banyak cara berbeda sesuatu bisa terjadi.
sedang mencari Seragam Sekolah? cek produk kami disini
lihat juga sosial media kita di instagram


